[[378304]]

十大經(jīng)典排序算法-希爾排序,歸并排序,快速排序前言這是十大經(jīng)典排序算法詳解的第二篇,這是之前第一篇文章的鏈接:十大經(jīng)典排序算法詳解(一)冒泡排序,選擇排序,插入排序,沒有看過的小伙伴可以看一下.

每次講解都是「先采用文字」的方式幫助大家先熟悉一下算法的基本思想,之后我會在通過「圖片的方式」來幫助大家分析排序算法的動態(tài)執(zhí)行過程,這樣就能夠幫助大家更好的理解算法.

每次的圖畫起來都比較的繁瑣,真的很耗費時間.所以如果你覺得文章寫得還可以或者說對你有幫助的話,你可以選擇一鍵三連,或者選擇關(guān)注我的公眾號:「萌萌噠的瓤瓤」 ,這對我真的很重要.UP在此謝謝各位了.

廢話不多說了,下面開始我們的正文部分吧!!!

1-希爾排序

算法思想:

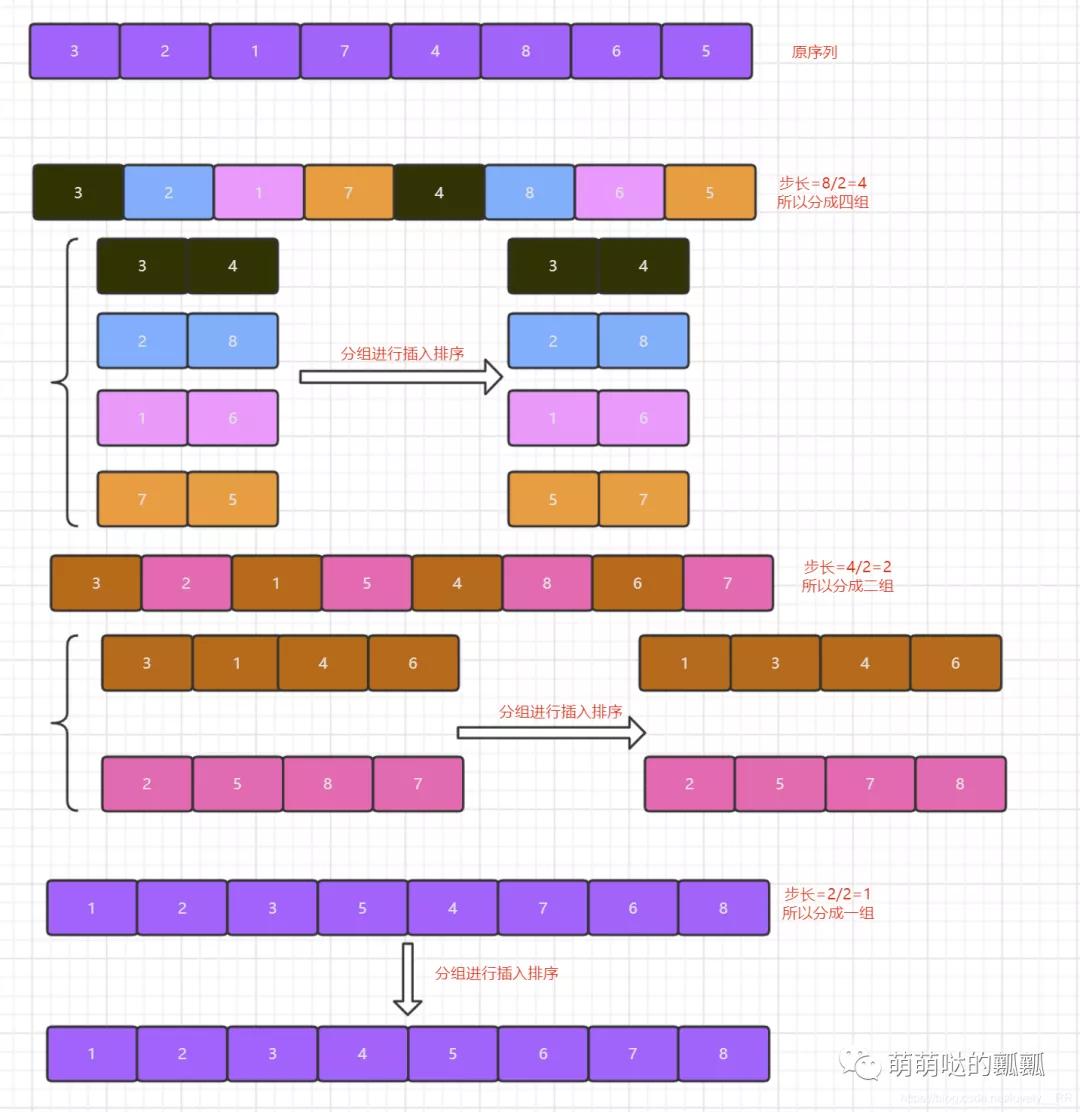
其實希爾排序的思想很簡單,因為希爾排序的基本思想就是第一篇中間講解的關(guān)于插入排序的基本思想,「只是希爾排序相比較與插入排序多加了一步就是確定步長」.之前在插入排序的過程中,我們的步長是固定的即為1,在希爾排序中我們的步長是不固定的,「一開始數(shù)組長度的一半,之后每次分組排序之后步長就再減半,直到步長到1為止」.這時候我們的排序就已經(jīng)完成了.

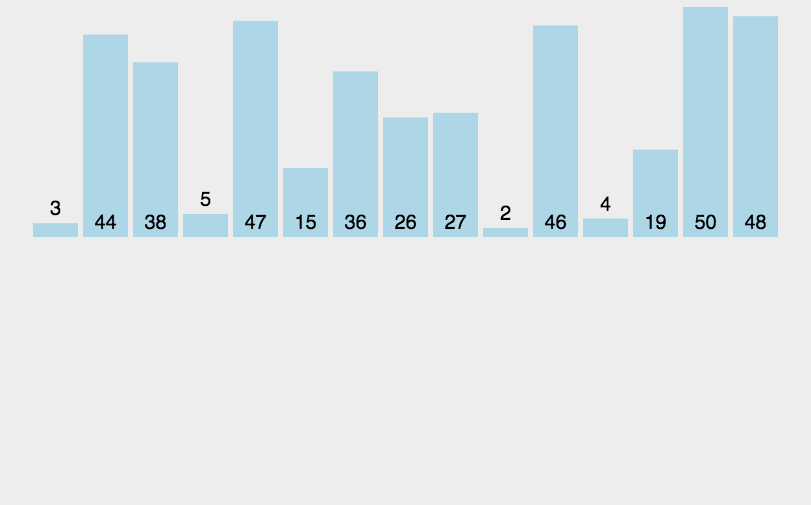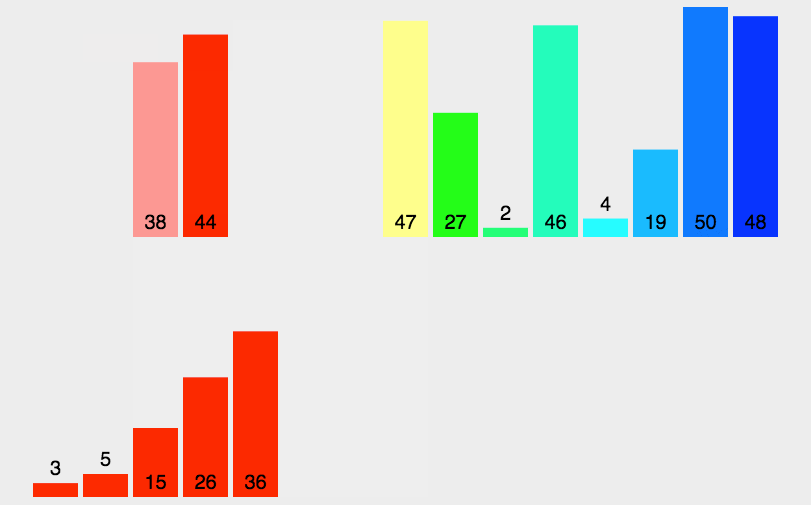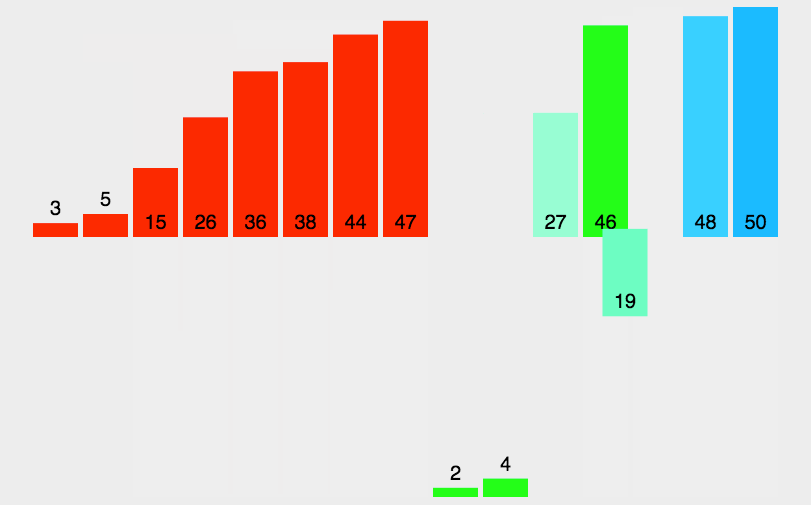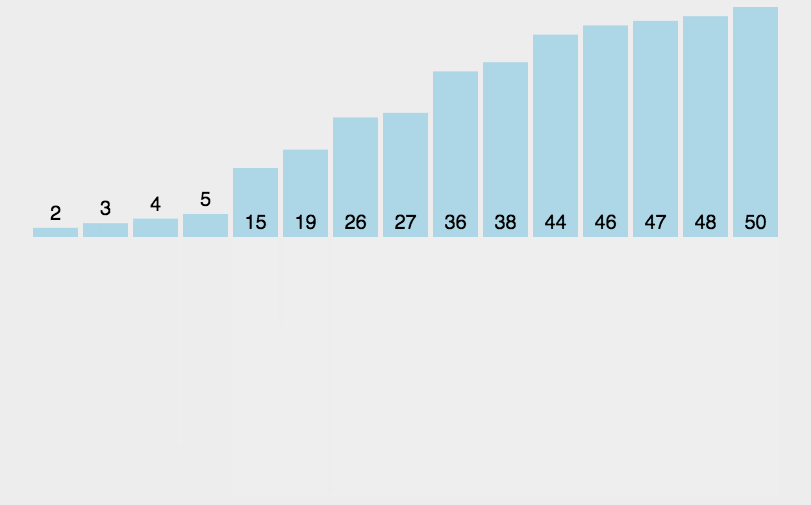
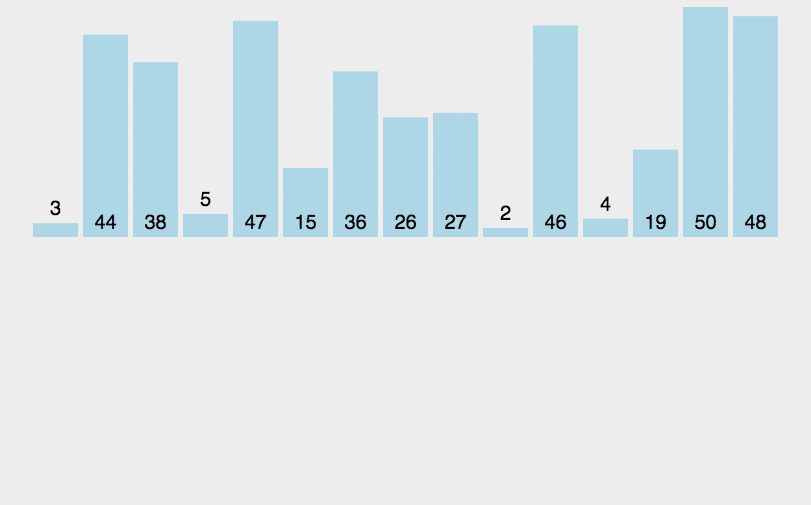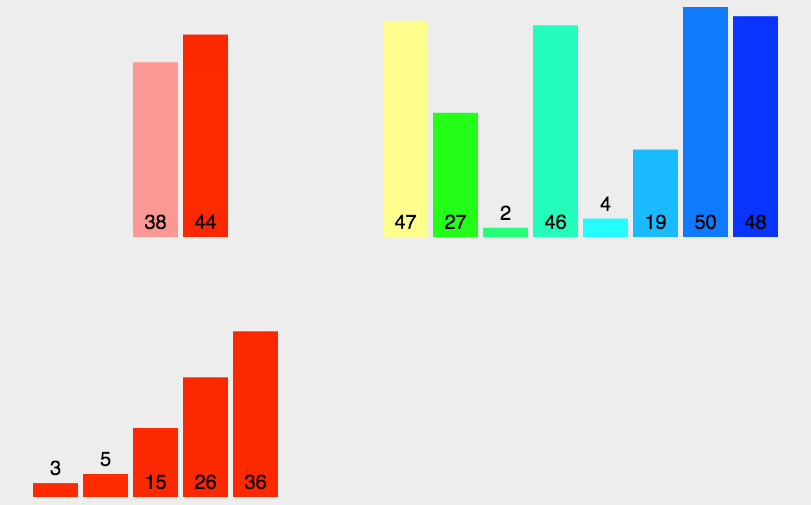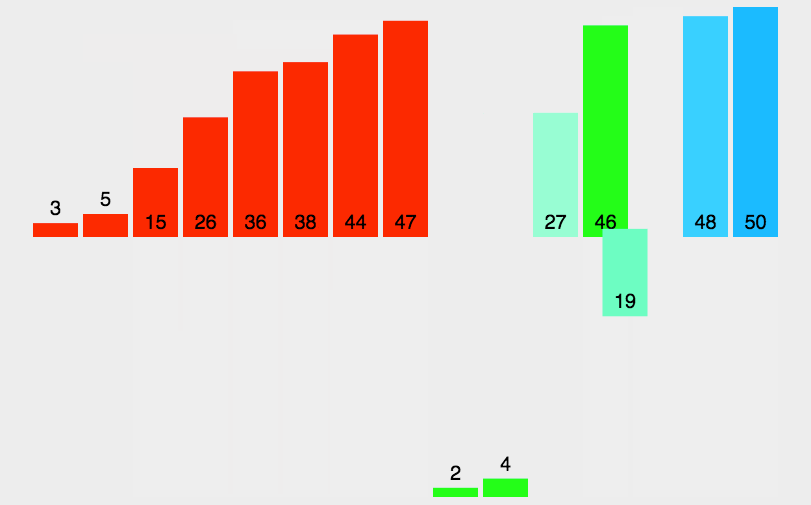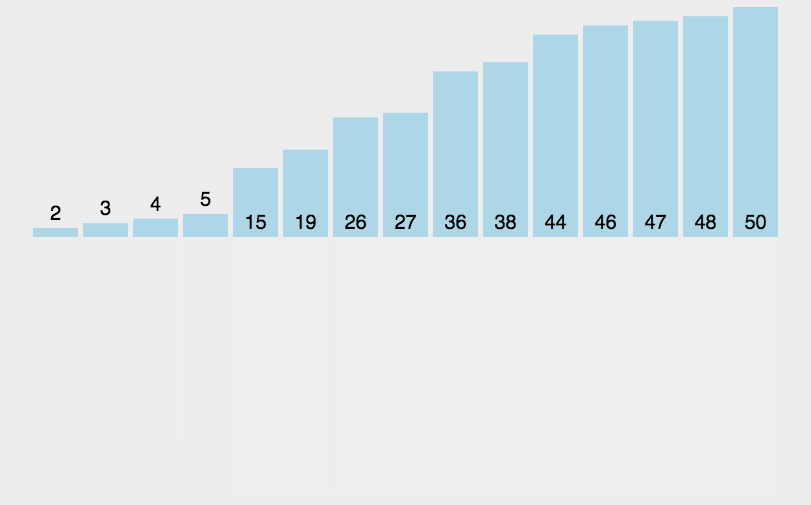
說完了,那我們接下來還是通過圖解的方式來幫助大家更好的理解希爾排序吧:

看完上面的圖之后相信大家就基本了解希爾排序算法的思想了,那么接下來我們還是來分析一下希爾排序算法的特點吧:

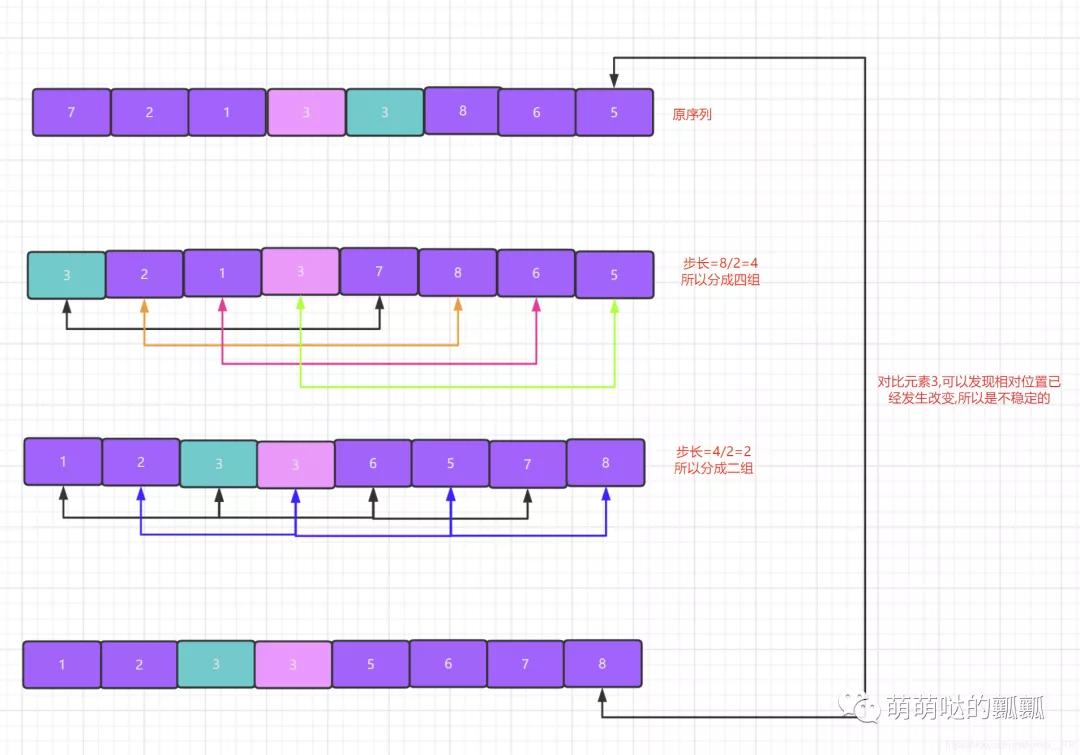
• 希爾排序算法是不穩(wěn)定的,這里大家可能會產(chǎn)生這樣的疑問,本身希爾排序算法的本質(zhì)就是插入排序,只不過是多了一步確定步長的過程,為什么插入排序就是穩(wěn)定的,但是希爾排序缺失不穩(wěn)定的呢?其實重點就是在分組之后,大家都知道在一個分組里面進行一次插入排序肯定是穩(wěn)定的,關(guān)鍵就在于希爾排序的過程中會出現(xiàn)多次分組,那么就會出現(xiàn)在之前的分組里面是穩(wěn)定的,但是到下一次分組的時候就會出現(xiàn)不穩(wěn)定的情況.

說這么多還不如直接來個例子給大家看一下,大家就知道了:

• 希爾排序是 「第一個」 在時間復雜度上突破O(N*N)的算法,這一點是非常有意義的.時間復雜度僅為O(N*log N)

算法圖解:

在這里插入圖片描述

示例代碼:

「按照算法思想不改動的版本」:

public static void main(String[] args) { 
  int []num ={7,4,9,3,2,1,8,6,5,10}; 
  long startTime=System.currentTimeMillis();  
  //規(guī)定步長 
  for(int step=num.length/2;step>0;step/=2) { 
   System.out.println("步長為"+step+"的分組排序:"); 
   //步長確定之后就需要分批次的對分組進行插入排序 
   for(int l=0;l<step;l++) { 
    //插入排序的代碼 
    for(int i=l+step;i<num.length;i+=step) { 
     int temp=num[i]; 
     int j=i; 
     while(j>0&&temp<num[j-step]) { 
      num[j]=num[j-step]; 
      j-=step; 
      //這里需要注意一點就是j-step可能會越界,所以我們需要繼續(xù)進行判斷 
      //之前在插入排序中,步長始終是1,所以在while循環(huán)那里就會阻斷,但是現(xiàn)在步長會發(fā)生變化 
      //所以我們需要在這里提前進行判斷,否則金輝發(fā)生數(shù)組越界的情況 
      if(j-step<0) 
       break; 
     } 
     if(j!=i) { 
      num[j]=temp; 
     } 
    } 
    System.out.println("   "+l+"號分組排序:"); 
    for(int k=0;k<num.length;k++) 
     System.out.print(num[k]+" "); 
    System.out.println(); 
   } 
   System.out.println(); 
  } 
  long endTime=System.currentTimeMillis();  
  System.out.println("程序運行時間： "+(endTime-startTime)+"ms");  
 } 

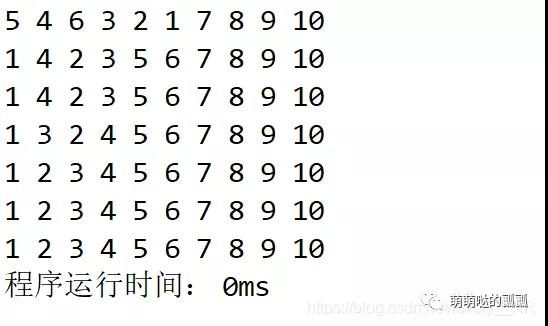
但是大家會發(fā)現(xiàn)如果真的按照希爾排序的思想這樣做得的話,我們會發(fā)現(xiàn)用了三層for循環(huán),那么很顯然時間復雜度就會達到我們目前遇到的最壞的情況即O(N*N*N),所以我們需要進行改進,主要就是改進分組排序的過程,之前我們是確定完步長之后,就通過for循環(huán)進行循環(huán)分組的排序,這里我們修改成直接和下一個for循環(huán)一起,直接進行循環(huán)分組

「改進后的代碼」:

public static void main(String[] args) { 
  int []num ={7,4,9,3,2,1,8,6,5,10}; 
  long startTime=System.currentTimeMillis();   
  for(int step=num.length/2;step>0;step/=2) { 
   System.out.println("步長為"+step+"的分組排序:"); 
   System.out.println("循環(huán)分組排序:"); 
   for(int j=step;j<num.length;j++) { 
    int temp=num[j]; 
    int k=j; 
    while(k-step>=0&&temp<num[k-step]) { 
     num[k]=num[k-step]; 
     k-=step; 
    } 
    num[k]=temp; 
    for(int l=0;l<num.length;l++) 
     System.out.print(num[l]+" "); 
    System.out.println(); 
   } 
  } 
  long endTime=System.currentTimeMillis();  
  System.out.println("程序運行時間： "+(endTime-startTime)+"ms");  
 } 

改進之后的算法之使用了兩層for循環(huán),真的讓時間復雜度達到了O(N*log N)

復雜度分析: 理解完希爾排序的基本思想之后,我們就需要來分析一下他的時間復雜度,空間復雜度.

• 時間復雜度

希爾排序的時間復雜度在各情況下,主要就取決于元素的個數(shù)以及分組的次數(shù),我們分析得到分組的次數(shù)剛好就是log N,所以我們可以得到希爾排序的時間復雜度僅為O(N*log N)

• 空間復雜度

這個我們可以看到我們整個排序的過程中只增加一個存儲Key的位置,所以希爾排序的空間復雜是常量級別的僅為O(1).

2-歸并排序

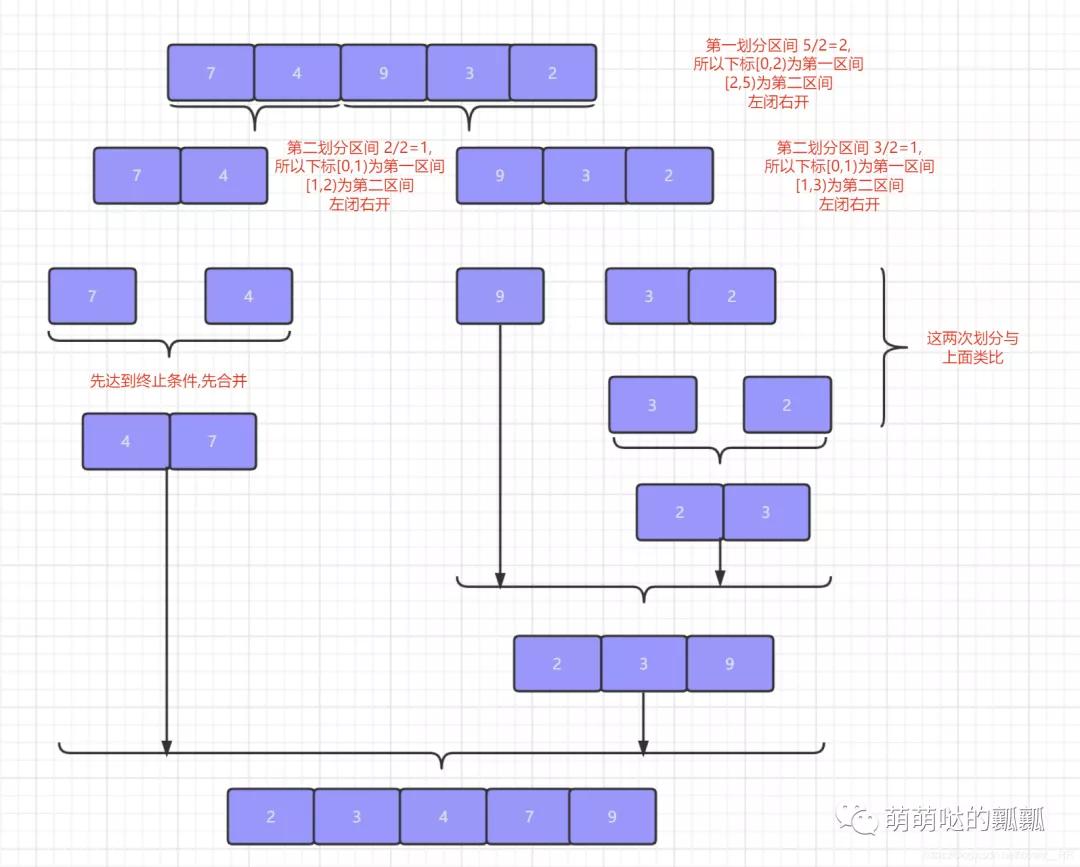
算法思想: 歸并排序的思想本質(zhì)就是進行分冶.把 「整個序列拆分成多個序列」,先將每個序列排好序,這個就是「分冶思想中分」,同樣也是「歸并排序中歸」 的思想.

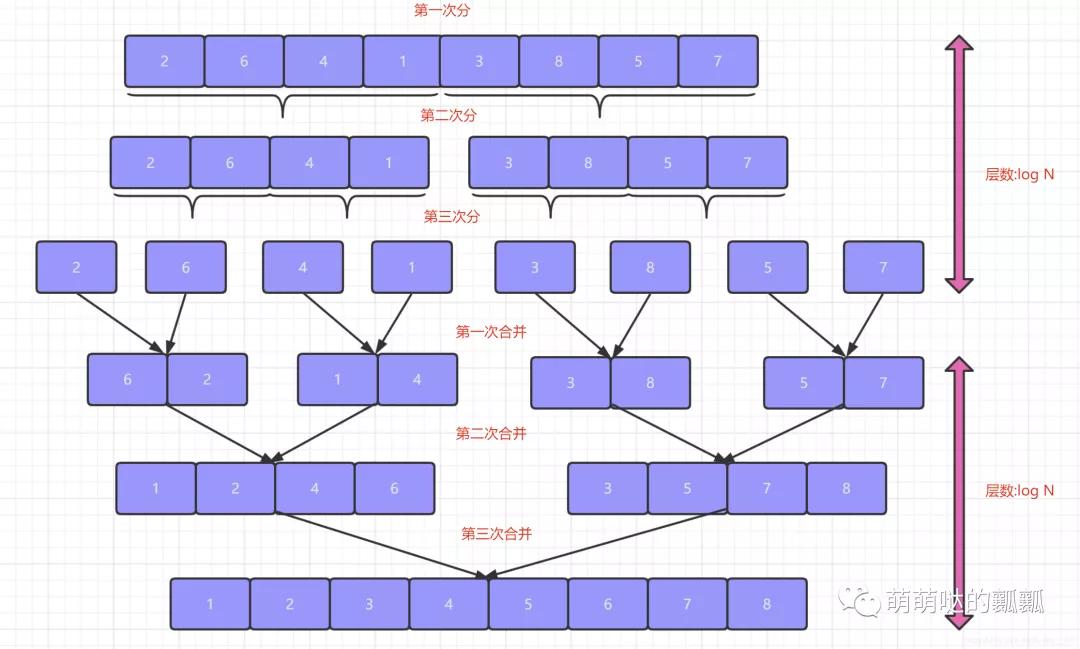
之后再將各個序列整合到一起這就是「分冶中的冶同樣也是歸并排序的并」.思想說完了,但是呢說不能解決問題,我們還是通過下面的圖來幫助大家理解:

看到圖之后,我們就會發(fā)現(xiàn)上面分和合并的過程都特別像遞歸對不對,都是按照一定的終止條件一直執(zhí)行下去.所以呢這就暗示了我們的歸并排序是可以通過「遞歸」的思想來編寫的.

現(xiàn)在我們基本上已經(jīng)基本了解歸并排序的基本思想了,現(xiàn)在我們再來看看歸并排序由那些特點吧

歸并排序是穩(wěn)定的,這個大家看過我上面的演示過程就能看出來了.

歸并排序需要消耗大量的內(nèi)存空間.這個內(nèi)存空間是對比冒泡排序之類的排序算法而言的,因為他們的內(nèi)存空間都是只存在于常量級別的,但是歸并排序卻是需要消耗線性級別的內(nèi)存空間,所以才會使用大量這個形容詞.消耗的內(nèi)存空間就是等同于待排序序列的長度.即O(n)的復雜度.

算法圖解:

在這里插入圖片描述

示例代碼:

重要代碼我已經(jīng)添加了注釋能夠更加方便讀者們理解.

public static int[] sort(int []num) { 
        //分裂之后的數(shù)組如果只有1個元素的話, 
        //那么就說明可以開始合并的過程了,所以直接返回. 
  if(num.length<2) 
   return num; 
  int middle=num.length/2; 
  //截取左右兩個序列 
  int []left=Arrays.copyOfRange(num, 0, middle); 
  int []right=Arrays.copyOfRange(num, middle, num.length); 
  return merge(sort(left), sort(right)); 
 } 
 public static int[] merge(int []left,int []right) { 
  int []num=new int [left.length+right.length]; 
  int i=0,j=0,k=0; 
  //注意終止條件是&&,只要有一個不滿足,循環(huán)就結(jié)束 
  while(i<left.length&&j<right.length) { 
   if(left[i]<right[j]) 
    num[k++]=left[i++]; 
   else  
    num[k++]=right[j++]; 
  } 
  //上面的循環(huán)跳出之后,就說明有且僅會有一個序列還有值了 
  //所以需要再次檢查各個序列,并且下面的兩個循環(huán)是互斥的,只會執(zhí)行其中的一個 
  //或者都不執(zhí)行 
  while(i<left.length) { 
   num[k++]=left[i++]; 
  } 
  while(j<right.length) { 
   num[k++]=right[j++]; 
  } 
  for(int l=0;l<num.length;l++) 
   System.out.print(num[l]+" "); 
  System.out.println(); 
  return num; 
 } 
 public static void main(String[] args) { 
  int []num ={7,4,9,3,2,1,8,6,5,10}; 
  long startTime=System.currentTimeMillis();   
  num=sort(num); 
//  for(int i=0;i<num.length;i++) { 
//   System.out.print(num[i]+" "); 
//  } 
//  System.out.println(); 
  long endTime=System.currentTimeMillis();  
  System.out.println("程序運行時間： "+(endTime-startTime)+"ms");  
 } 

這里呢就不演示全部的元素了,這里就簡單和大家演示一下左半邊區(qū)間元素排序的過程,右半邊大家可以自行腦補,這個應該不難.

這樣大家應該就能理解了,主要就是如果「序列長度不是2的次方」的話,后續(xù)劃分序列的時候就會出現(xiàn)上述與我們類似的情況.畢竟我們劃分區(qū)間的 整個過程就類似于「將區(qū)間中心劃分成一個二叉樹」.

復雜度分析:

理解完歸并排序的基本思想之后,我們就需要來分析一下他的時間復雜度,空間復雜度.

• 時間復雜度

其實我們從上面的算法中能明顯看出來我們沒有使用for循環(huán),而是通過遞歸的方式來解決我們的循環(huán)問題的.所以更加的高效. 就像我們上面的演示過程里面寫的一樣,這個執(zhí)行的層數(shù)為2 * log N,并且每層操作的元素是N個,所以我們的時間復雜度即為2 * N * log N,但是常數(shù)可以忽略不計,所以我們的時間復雜度就控制在了O(N*log N),對比我們之前算法的時間復雜度O(N*N),可以看到「時間復雜度明顯降低很多」,并且這個時間復雜度「不僅僅只是適用于平均情況,針對最壞的情況,同樣也能適用」.

• 空間復雜度

這個我們也可以看到我們整個排序的過程中需要增加一個等同于排序序列的長度的空間來存儲我們?yōu)槎闻判蛑蟮男蛄?所以我們需要的空間復雜度就是線性級別的O(n),這個復雜度對比我們之前的幾種排序算法,可以看得出來的確是較為大了一點.但是也可以明顯看出來整個的時間復雜度明顯降低了很多,這就是一種跟明顯通過犧牲空間換取時間的方法.對比我們第一篇講的HashMap.

3-快速排序

算法思想:

快速排序的算法思想也比較好理解.但是呢用文字講述出來可能會有點難以理解,這里我盡可能的講的簡單些.就算還是看不懂的話也沒事,我們還是會通過圖片演示的形式來加深大家的理解的.

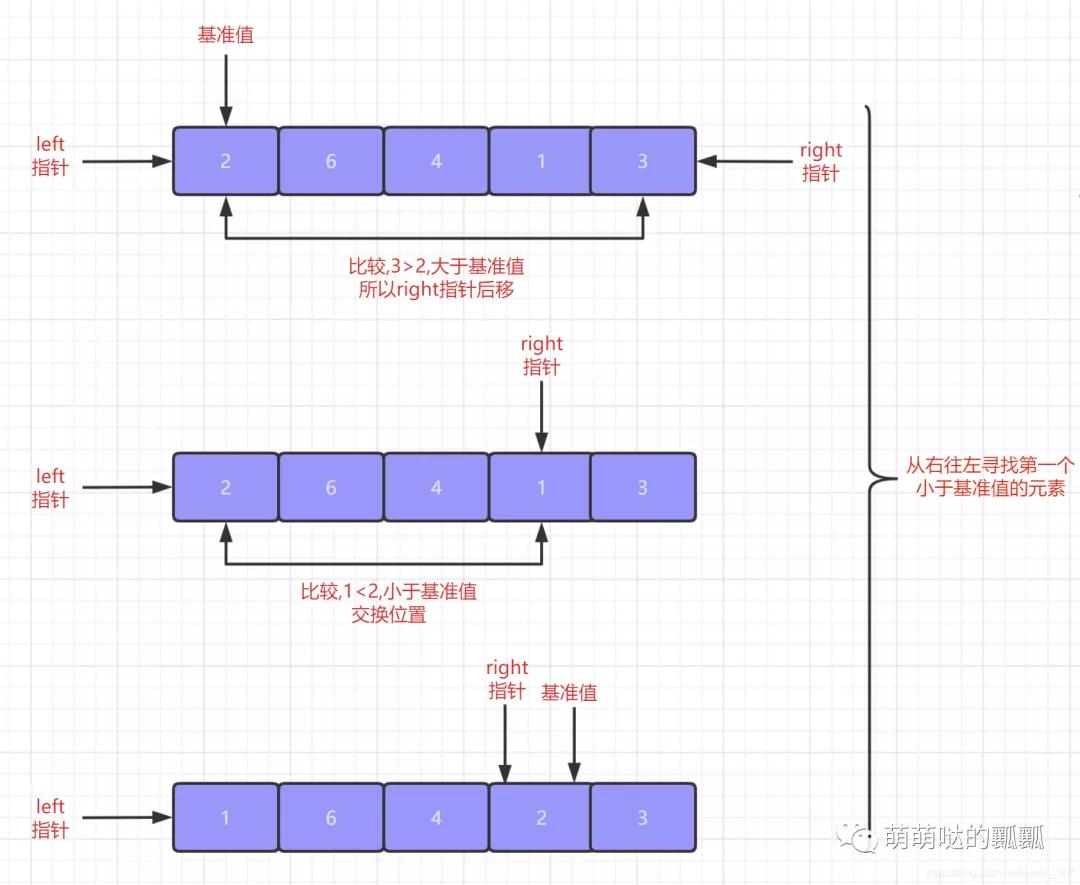
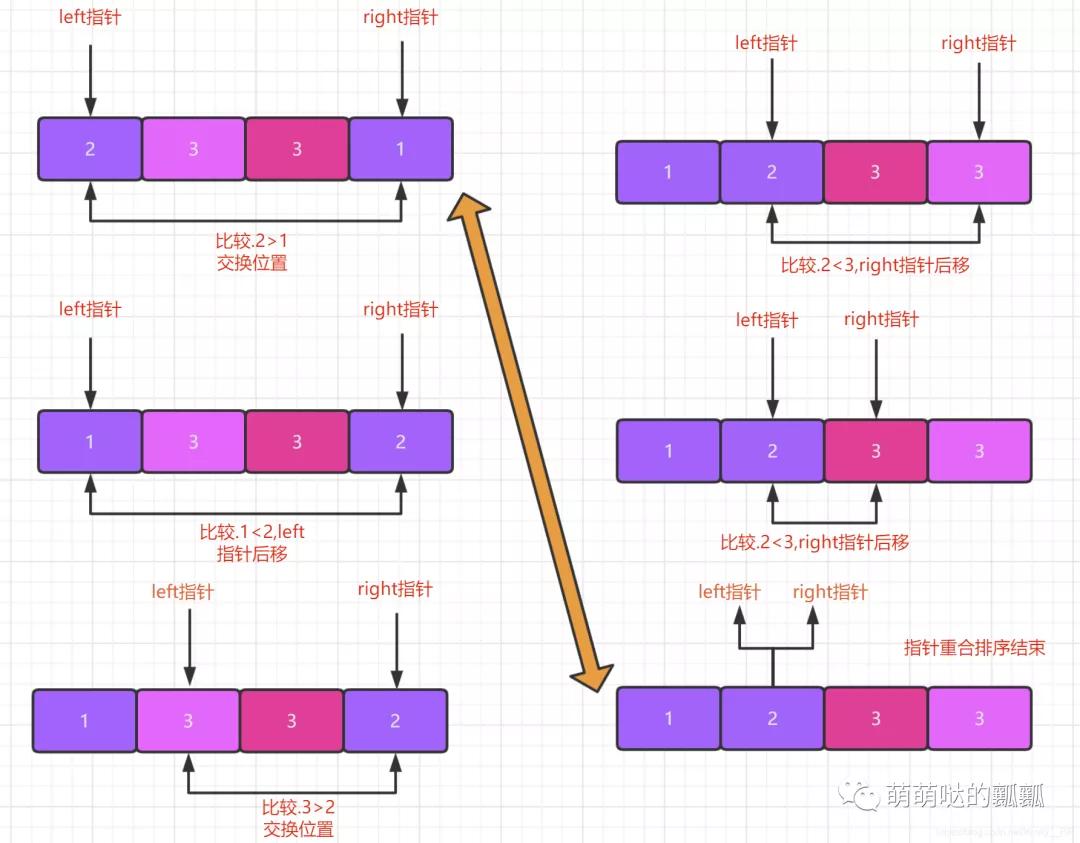
快速排序的思想就是每次排序都「選定一個基準值」 ,當我們在選定完這個基準值之后,我們就另外在需要兩個""指針"",這個指針并不是我們C++中的指針,但是作用也差不多,主要就是幫助我們標記位置的.「這兩個指針分別指向待排序序列的隊頭元素和隊尾元素」.

我們首先先「從隊尾元素開始從右往左查找出第一個不大于該基準值的元素」,找到之后首先將之前指向隊尾元素的指針指向該元素位置,之后再將基準值與我們剛才查找到的元素交換位置.

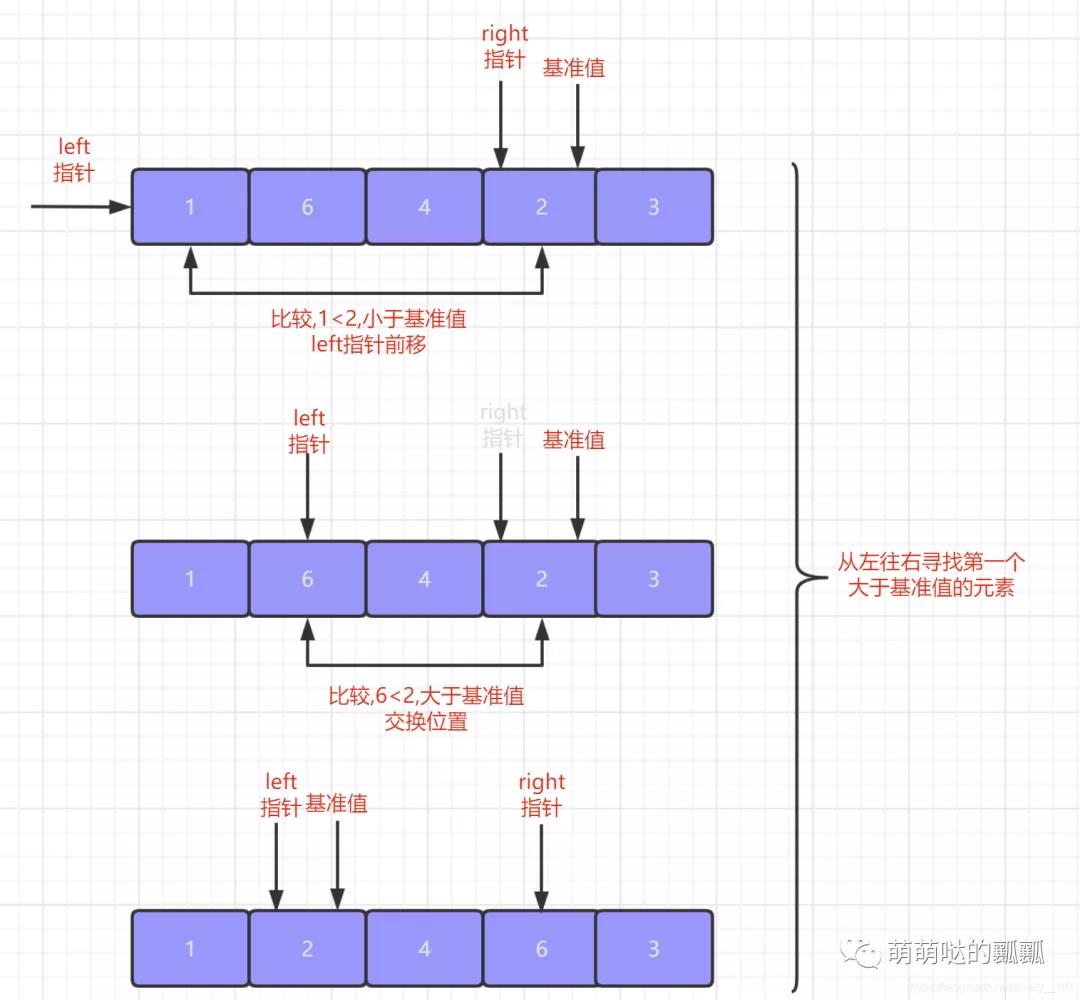
在這個步驟結(jié)束之后,我們就需要「從隊頭元素開始從左往右查找第一個不小于基準值的元素」,查找到該元素之后還是按照我們上面的步驟.先將之前指向隊頭元素的指針指向該元素,之后再將基準值與該元素交換位置.

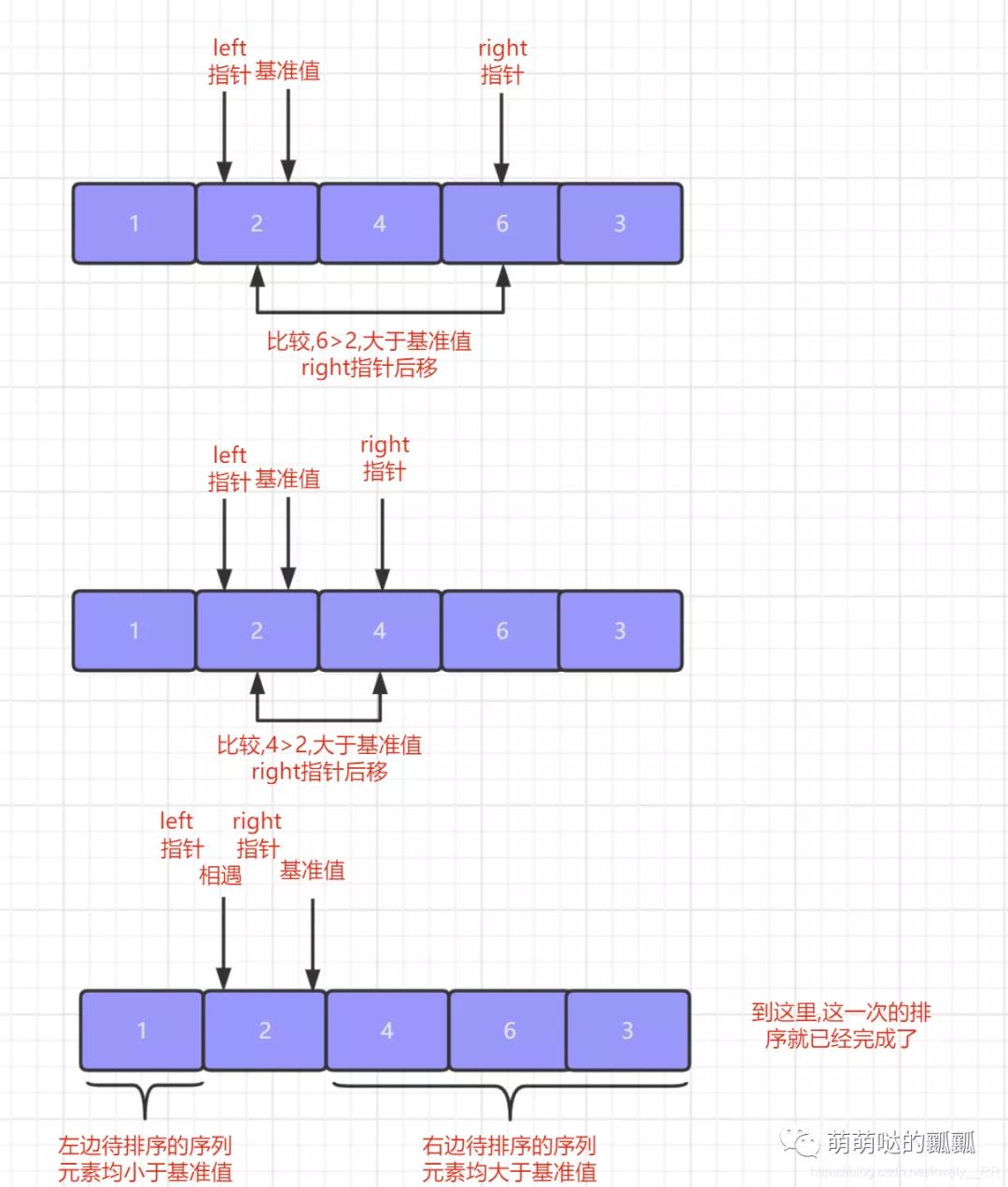
重復上面這個步驟,「直到隊頭指針與隊尾指針相遇,相遇之后就代表我們的第一次排序就已經(jīng)完成了」,并且在第一次排序完成之后我們就會發(fā)現(xiàn)序列是這樣的狀態(tài),「基準值左邊的元素全部小于等于該基準值,基準值右邊的元素全部大于等于該基準值.」

之后的排序就只需要對基準值左右兩邊的序列在進行上述的操作即可.

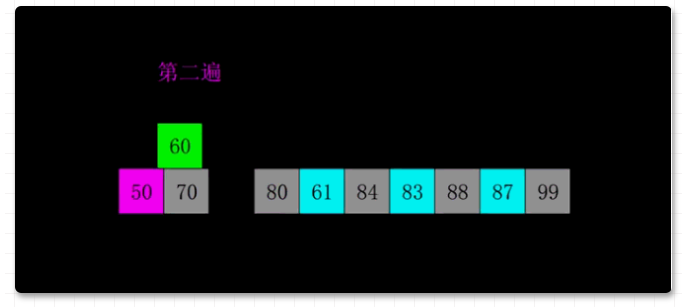
好了關(guān)于算法的文字講解已經(jīng)完成了,當然了,這時候很多小伙伴肯定會想 「"你這都說的啥啊"」 ,沒關(guān)系老樣子還是用圖來說話:

這里我只演示了第一次排序的過程,后續(xù)的相信大家可以自行腦補的. 理解完快速排序的基本算法思想之后,我們就需要來稍微聊聊快速排序的特點了.

快速排序本身是不穩(wěn)定的,我們首先先來了解一下不穩(wěn)定的快排是什么樣的演示過程.

通過上面的圖大家就能知道快排為啥是不穩(wěn)定的了.

「快速排序也有一個極端情況」,就是快排在對 「已經(jīng)有序的序列進行排序」的時候,時間復雜度會直接飆到O(n*n),也就是最壞的時間復雜度,這個情況大家其實自己模擬以下就能知道了. 這里我們就不在過多講解了.算法圖解:

在這里插入圖片描述

示例代碼:

重要代碼我已經(jīng)添加了注釋能夠更加方便讀者們理解.

public static void sort(int []num,int left,int right) { 
  if(left<right) { 
   int key=num[left]; 
   int i=left; 
   int j=right; 
   //這部分便是算法的核心思想 
   while(i<j) { 
    //從右向左找到第一個不大于基準值的元素 
    while(i<j&&num[j]>=key) { 
     j--; 
    } 
    if(i<j) { 
     num[i]=num[j]; 
    } 
    //從左往右找到第一個不小于基準值的元素 
    while (i<j&&num[i]<=key) { 
     i++; 
    } 
    if(i<j) { 
     num[j]=num[i]; 
    } 
   } 
   num[i]=key;  
   for(int k=0;k<num.length;k++) { 
    System.out.print(num[k]+" "); 
   } 
   System.out.println(); 
   //遞歸繼續(xù)對剩余的序列排序 
   sort(num, left, i-1); 
   sort(num, i+1, right); 
  }  
 } 
 public static void main(String[] args) { 
  int []num ={7,4,9,3,2,1,8,6,5,10}; 
  long startTime=System.currentTimeMillis();  
  sort(num, 0, num.length-1); 
  long endTime=System.currentTimeMillis();  
  System.out.println("程序運行時間： "+(endTime-startTime)+"ms");  
 } 

因為上面的動態(tài)演示圖已經(jīng)演示的很清楚了,所以就不在畫圖演示了.

復雜度分析:

理解完快速排序的基本思想之后,我們就需要來分析一下他的時間復雜度,空間復雜度.

• 時間復雜度

其實我們從上面的算法中能明顯看出來我們沒有使用for循環(huán),而是通過遞歸的方式來解決我們的循環(huán)問題的.所以更加的高效.

就像我們上面所演示的一樣,平均情況下的時間復雜度即為O(N * log N),但是也想我們所說的那樣,快速排序存在著一個極端情況就是 「已經(jīng)有序的序列進行快排」 的話很剛好形成是類似于冒泡排序一樣的時間復雜度即為O(N * N),這是我們需要注意的,但是在大多數(shù)情況下,快排還是我們效率最高的排序算法.

• 空間復雜度

這個我們也可以看到我們整個排序的過程中每次排序的一個循環(huán)里面就需要添加一個空間來存儲我們的key,并且快排其實和我們上面的歸并排序也是有異曲同工之妙的,也有點類似于使用了二叉樹的概念,所以他的空間復雜度就是O(log N)

到這里十大經(jīng)典排序算法詳解的第二期內(nèi)容就已經(jīng)結(jié)束了.如果覺得UP的文章寫得還可以或者對你有幫助的話,可以關(guān)注UP的公眾號,新人UP需要你的支持!!!