[[393503]]

基本介紹

歸并排序(merge-sort)是利用歸并的思想實現(xiàn)的排序方法,該算法采用經典的分治(divide-and-conquer)策略(分治法將問題分(divide)成一些小的問題然后遞歸求解,而治(conquer)的階段則將分的階段得到的答案"修補"在一起,即分而治之).

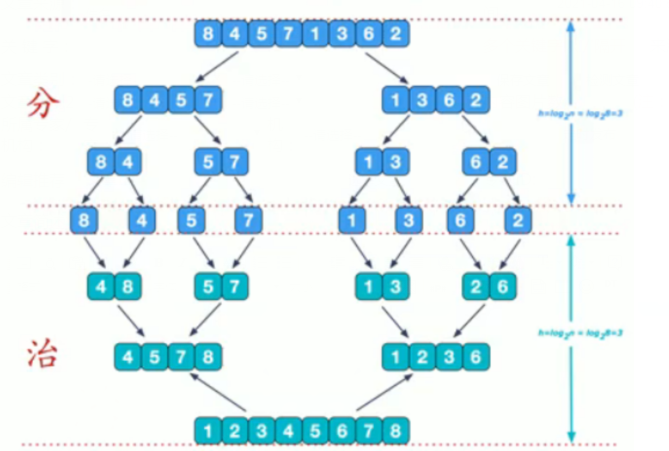
示意圖

說明:可以看到這種結構很像一顆完全二叉樹,本文的歸并排序我們采用遞歸去實現(xiàn)(也可以采用迭代的方式去實現(xiàn)).分階段可以理解為就是遞歸拆分子序列的過程.

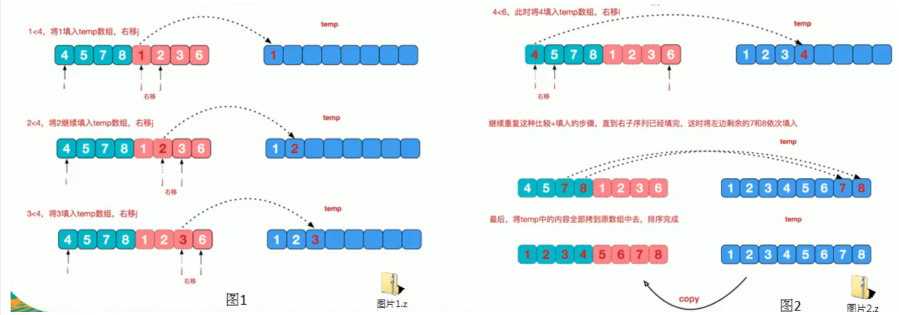
再來看看治階段,我們需要將兩個已經有序的子序列合并成一個有序序列,比如下圖的最有一次合并,要將[4,5,7,8]和[1,2,3,6]兩個已經有序的子序列,合并為最終序列[1,2,3,4,5,6,7,8],來看下實現(xiàn)步驟.

代碼示例

package com.structures.sort; 
 
blic class MergeSort { 
  public static void main(String[] args) { 
      int[] arr = new int[80000]; 
      for (int i = 0; i < 80000; i++) { 
          arr[i] = (int) (Math.random() * 8000000); 
      } 
      int[] temp = new int[arr.length]; 
      long start = System.currentTimeMillis(); 
 
      mergeSort(arr,0,arr.length-1,temp); 
      long end = System.currentTimeMillis(); 
      System.out.println("耗時:" + ((end - start)) + "ms"); 
      /* 
      耗時:15ms 
       */ 
  } 
 
  //分+合 
  public static void mergeSort(int[] arr, int left, int right, int[] temp) { 
      if (left < right) { 
          int mid = (left + right) / 2; 
          //向左遞歸進行分解 
          mergeSort(arr, left, mid, temp); 
          //向右遞歸進行分解 
          mergeSort(arr, mid + 1, right, temp); 
          //合并 
          merge(arr, left, mid, right, temp); 
      } 
  } 
 
  /** 
   * 合并 
   * @param arr   已排序的原始數(shù)組 
   * @param left  左邊有序序列的初始索引 
   * @param mid   中間索引 
   * @param right 右邊索引 
   * @param temp  做中轉數(shù)組 
   */ 
  public static void merge(int[] arr, int left, int mid, int right, int[] temp) { 
      int i = left;//初始化i,左邊有序序列的初始索引 
      int j = mid + 1;//初始化j,右邊有序序列的初始索引 
      int t = 0;//指向temp數(shù)組的當前索引 
 
      //(一) 
      //先把左右兩邊(有序)的數(shù)據(jù)按照規(guī)則填充到temp數(shù)組 
      //直到左右兩邊的有序序列,有一邊處理完畢為止,即全部填充到temp數(shù)組 
      while (i <= mid && j <= right) { 
          //如果左邊的有序序列小于等于右邊的有序序列的當前元素 
          //即將左邊的當前元素拷貝到temp數(shù)組 
          //然后t++,i++后移 
          if (arr[i] <= arr[j]) { 
              temp[t] = arr[i]; 
              t += 1; 
              i += 1; 
          } else {//反之,將右邊有序序列的當前元素,填充到temp數(shù)組 
              temp[t] = arr[j]; 
              t += 1; 
              j += 1; 
          } 
      } 
 
      //(二) 
      //把有剩余數(shù)據(jù)的一邊的數(shù)據(jù)依次填充到temp 
      while (i <= mid) {//左邊的還有剩余,填充到temp數(shù)組 
          temp[t] = arr[i]; 
          t += 1; 
          i += 1; 
      } 
      while (j <= right) { 
          temp[t] = arr[j]; 
          t += 1; 
          j += 1; 
      } 
 
      //(三) 
      //將temp數(shù)組的元素拷貝到arr 
      //注意并不是每次都拷貝所有 
      //第一次合并leftTemp = 0,right = 1,第二次合并leftTemp = 2,right = 3,第三次合并leftTemp = 0,right = 3... 
      t = 0; 
      int leftTemp = left; 
      while (leftTemp <= right) { 
          arr[leftTemp] = temp[t]; 
          leftTemp += 1; 
          t += 1; 
      } 
  } 

 【編輯推薦】